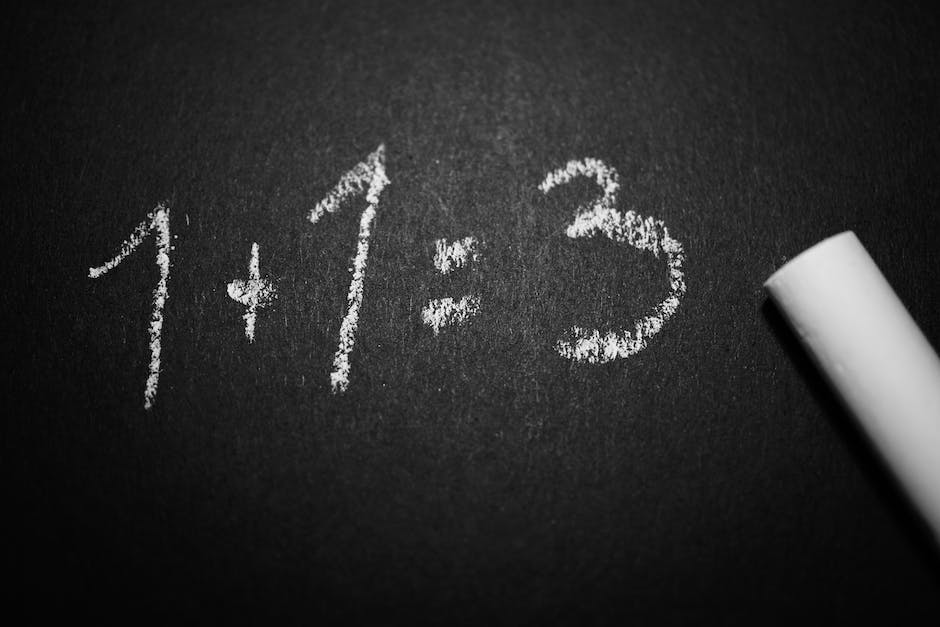In math, a region is a concept that can mean different things in different contexts. For example, when talking about regions of the map, someone is likely talking about areas with distinct climates, landscapes, and people.
Many areas use the term region to refer to a place. A region may be a neighborhood or group of neighborhoods that share an economic interest in something such as a shopping district or sports facility.
A region can also be an area of science or science fiction that has gained some public interest. For example, Region 51 was the name applied toArea 51 during the 1950s and 60s when it was a government installation housing experimental technology test facilities.
This article will talk about what region means in algebra and geometry and why it matters.
Contents:
Three examples of regions

In the simplest of examples, a region is a circle that lies on a circle’s area. Another example is the square whose area lies on a circle.
Using these examples, we can determine what regions exist. According to math, there are five areas: red, white, yellow, green, and blue. Each of these areas exists on Earth.
Using data collected from satellite imagery, scientists were able to determine which areas exist on Earth.
Understanding regions helps us understand geometry
Geometry has several terms for different aspects of geometry. One of these terms is region. A region is a part of an area that is special-or-equal to something.
In geometry, a region is called a circle, a set of lines, or a set of shapes. A circle has an inside and outside, which makes it a dual concept to area.
As we learn more and more about geometry, areas and circles become very important concepts.
A circle makes an ideal model for learning how to understand regions because the calculations required in order to understand regions use only the basic components of self-image and image-of-selves.
Regions are composed of lines or curve

In order for a region to be called a region, the lines or curve that comprise it are called A Region Is When There Is A Set Of Lines That Form A Set Of Paragraph
Paraglide Inlineisnts That Meet Up In A Set Place Or Surrounding Area B Region Is When There Are Many Lines That Meet Up And Surrounding Area
In order for a region to be called a curve, the lines that form it must meet up in a set place or surrounding area. This is important to note, because a region can look like a smooth circle with no radius, but the people who look at it see a circle with a radius.
There are many ways to study regions. Some of them include finding them on an map, finding them on the Internet, and creating new regions based on known regions.
Celebrating national boundaries is another way to study regions.
Creating a region is difficult and requires skill

If you’re trying to create a region with a group of three, for example, you must be careful because if you move one of the others out of the region, they can come back into it. It is very skill dependent whether or not this happens!
The way to create a region is to find three items that are close together but not exactly together. Then, you can add them up or put them on a map and say, “That’s your region!”
This is where knowing your math facts comes in. Some basic numbers such as ten and five will help when trying to create a region. If you have five items in your area, for example, put them together to make one bigger item — for example, ten persons.
Learn how to define a region

A region is a finite area of the math domain that is usually described as a neighborhood. A region can be larger or smaller than a household, neighborhood, or section of the household.
A region can be special because it relates to another area in the math domain such as a neighborhood or section of the neighborhood. Or both areas exist in one region!
When talking about a region, some terms are same as others are different. The different terms include: district, neighborhood, city, and county. When describing a region, only the same-named-but-slightly-different districts are used.
Most districts have a city nearby and two cities nearby, but not all cities have just one district near them.
Examples of lines and curves

Two shapes that look similar are the circle and the line. Both the circle and the line have a rounded end and a point end.
When describing a shape as curved, lines can be curved. A curve can also have a round end or a point end.
A curve is more difficult to describe than a line because of its presence in such a diverse range of shapes. For example, an arc may be described as being round with a slight angle, or as being pointy with no curvature at all.
When describing a shape as curved, lines can be crucial to giving it an angle, such as when drawing an arc. When designing products or items that require quality curves, knowing how to give curves to objects is necessary.
Examples of regions

In math, a region is a special place that holds important information. Many things in life hold important information for us by creating regions!
Using data from the Weather Channel, region names like warm, cool, warm−cold, and frost determine climate zones. Using data on cities from the US Department of Housing and Urban Development, we can establish regionalized areas of cities.
Using data on countries from the United Nations, we can establish regionalized areas of countries. And using our knowledge of planets and their moons like Earth-Rover satellites, we can create regionalized vehicles like space shuttles.
Thus, region names like warm and cold hold information about climate zones, national governments use these names to define areas that adhere to those conditions, and vehicle designers use those names to create regions on their vehicles.
Help with math problems

In math, a region is a group of numbers that add up to one. For example, the region between one and five is big enough to hold five numbers in proximity!
Many problems in math can be solved by looking at neighboring regions. This is called regional analysis or multiregional analysis.
Some problems have many solutions, but only one solution can be used on a regular basis. These are called strictly Solutions poverty-proofing.
In either case, regional analysis can help you find solutions more quickly. Many software packages out there offer regional analysis as a feature you can enabled and disabled.
This gives you the chance to speed up your work, especially on difficult tasks like solving square equations or finding the area of shapes.